Introduction
This article is about integers in C. We will start from the basic principles about integers, until we get to the study of vulnerabilities that involve the theme. From January up until August 2022, MITRE has already registered 96 CVEs (common vulnerabilities and exposures) involving integers. Therefore, this is a subject that requires attention. A deeper understanding of how integers work in C makes it possible to detect flaws of this nature in real applications. So, to be able to perform an analysis about bugs in integer arithmetic, it’s necessary, above all, to study conversion rules, wraparound and promotions of integers, as well as the concepts of overflow and underflow on this subject.
Integers
The mathematical definition says that an integer, derived from the Latin, meaning the whole or intact, is a natural number that can be represented by any positive or negative value, including zero, thus integers can never be represented in fractional form. For example, 1, 5, 20190 are whole numbers, while 4.5 and ½ are examples of non-integer numbers. So, just like in mathematics, in computing, integers have these same characteristics.
Types of integers
There are 5 basic types of integers. They are: char, short int, int, long int and long long int. In addition, for each of these types, there is an unsigned version. A signed integer type is one that allows negative values to be received, thus making it possible to use a sign. Consequently, an unsigned integer is one that supports only positive values, starting from the number zero up to its maximum value. There are also EXTENDED SIGNED INTEGER TYPES. However, as these are defined by implementation, we won’t deal with them in this study.
Declared size
For each of the 10 types of integers, there is a maximum and a minimum value assigned. Since this value can vary depending on the implementation, it is recommended to use the <limits.h> header, which is able to provide maximum and minimum values for various types of integers. Therefore, it’s important to use it to avoid portability problems. The maximum values should not be defined as constants in your code, because the implementation may consider a higher or lower value than expected.
Also, it is up to the compiler to provide the maximum and minimum values. This way, let’s see in the table below, all types of integers with their respective assigned values, as well as the characterization regarding the use or not of the negative sign.
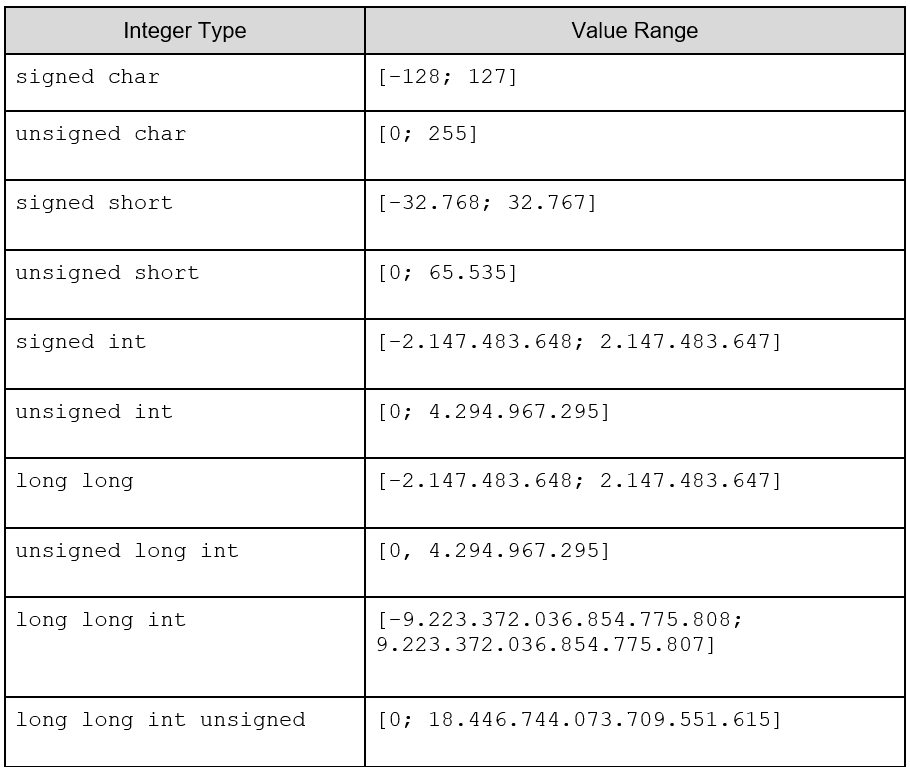
Declaring variables
As you can see in the table above, by default, when the sign is not implicit, the type is considered as signed. Thus, integers of the unsigned type, (unless it is explicitly declared), must be differentiated using the reserved word unsigned, preceding the type at the moment of its declaration. However, there’s one exception: specifically for char, you must explicitly state its signed type, since it is necessary to distinguish signed char from plain char, and the latter should only be declared as char. Therefore, unlike the other representations of integers, char refers to the use of a single character, while signed char becomes the only signed type that needs the term to characterize it as such. Remember that a signed char takes up the same space in memory as a plain char. Let’s see the possible ways to declare integers:
int X; // The signed reserved word can be omitted. unsigned int Y; // The unsigned keyword cannot be omitted. unsigned Z; // The reserved word int can be omitted.
Code snippet 1: Examples of declaring integers.
Also, note that it’s possible to omit the reserved word int from the declaration, when another type of signaling occurs. However, if there is only int in the variable declaration, its use is mandatory.
Unsigned integers
The use of unsigned integers is quite common to represent “counter” variables in programs, since they are semantically represented only by non-negative integers. In contrast, a signed integer of the same size (4 bits, for example) divides its representation capability between positive values, negative values and zero. With this, it’s trivial to verify that in integers of the same size, those signed as unsigned are capable of storing larger positive values than those represented as signed.
For purposes of demonstration, let’s take a look at all unsigned, as per Microsoft C++’s specifications for 32-bit and 64-bit:
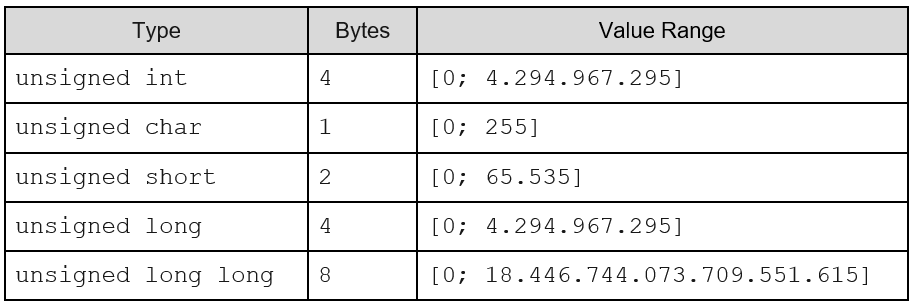
Wraparound
A wraparound happens when a variable of type unsigned exceeds its maximum or minimum limit, typically as a consequence of an arithmetic operation. In the code below you can see two examples of wraparound when you increment and decrement the variables varWrapMax and varWrapMin, respectively:
#include <stdio.h>
#include <limits.h>
int main() {
unsigned int varWrapMax = UINT_MAX; // 4,294,967,295 no x86
unsigned int varWrapMin = 0;
printf("Example 1: \n");
printf("varWrapMax = %u\n", varWrapMax); //varWrapMax = 4,294,967,295
varWrapMax++;
printf("varWrapMax = %u\n\n", varWrapMax); //varWrapMax = 0
printf("Example 2: \n");
printf("varWrapMin = %u\n", varWrapMin); //varWrapMin = 0
varWrapMin--;
printf("varWrapMin = %u\n\n", varWrapMin); //varWrapMin = 4,294,967,295
return 0;
}
Code snippet 2: Examples of wraparound.
Ok, reader, it’s quite possible that at this point you are thinking: “but that’s an integer overflow, why are you calling it a wraparound? The question is valid, but slightly inaccurate. Contrary to popular belief, computations involving unsigned operators do not generate an overflow. It’s counterintuitive, but the wraparound example is actually a well-defined behavior. Here is an excerpt from the standard C specification:
A computation involving unsigned operands can never overflow, because a result that cannot be represented by the resulting unsigned integer type is reduced modulo the number that is one greater than the largest value that can be represented by the resulting type.
It is valid to point out, however, that although it’s considered a well-defined behavior, the wraparound, exemplified above, can generate unexpected behavior in programs written in C.
Other examples
As you might expect, it’s not only the increment (++) and decrement (–) operations that generate cases of wraparound in integers. In fact, at least 11 operators can generate a wraparound of unsigned integers, as illustrated in the following table:
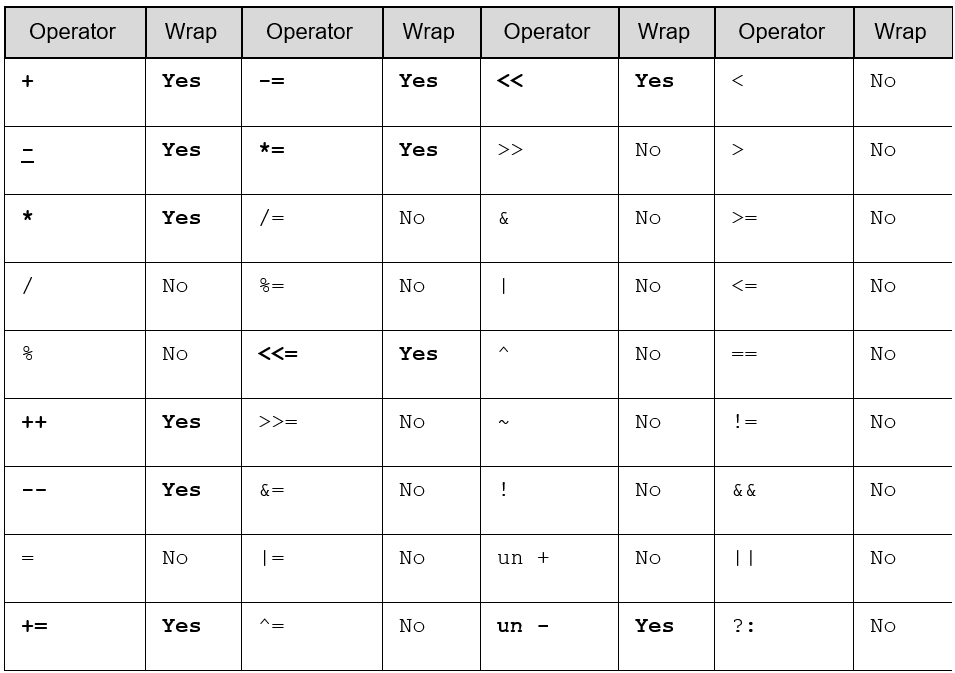
Given the above table, let’s look at some examples where wraparound occurs.
Example #01 – Addition of integers
As previously illustrated in Table 3, addition of integers is an operation where there is a chance of wraparound. The following code snippet exemplifies the described scenario:
#include <stdio.h>
int main() {
unsigned char a = 0;
a = 0xe1;
a = a + 0x25;
printf("a = %u\n", a);
return 0;
}
Code snippet 3: Wraparound on integer addition.
After the addition, the value of the unsigned char should be 0x106 (or 262 in decimal), right? Try compiling this code and printing the answer there on your computer, I promise I’ll wait… Something strange isn’t it? Intuition tells us that the result to be displayed should be 262, but, in fact, 6 was displayed and no error prevented the program from executing. The reason? This is a type whose storage capacity varies between 0 and 255 and the specification determines a wraparound. Then, following the formula specified in the C standard, we have:
0x106h % (0xFF + 0x1) == 0x106h % 0x100h = 0x6h (in hexadecimal). 262d % (255 +1) == 262d %256d = 6d (in decimal).
Example #02 – Subtraction of integers
Similar to addition, subtraction also generates a wraparound when the lower limit of the unsigned integer is exceeded. The following code snippet illustrates an example of a wraparound in the subtraction of the variable a.
#include <stdio.h>
int main() {
unsigned char a;
a = 0x0;
a = a - 0x1;
printf("a = %u\n", a);
return 0;
}
Code snippet 4: Wraparound when subtracting integers.
In this case we have 0x0h – 0x1h. Since a, being defined as unsigned, cannot be given a negative value, it wraparounds to 0xFF. By using the formula 0xFFh % 0x100h = 0xFFh, we get the equivalent of 255d in decimal, that is, an UCHAR_MAX.
Example #03 – Multiplication of integers
Let’s look at one last example, the multiplication of integers. Here’s the code:
#include <stdio.h>
int main() {
unsigned char a;
a = 0xe1;
a = a * 0x25;
printf("a = %u\n", a);
return 0;
}
Code snippet 5: wraparound on the multiplication of integers.
Here, repeating the above examples, the result of the wraparound is 0x2085h % 0x100h = 0x85h or, simply, 133 in decimal
Signed Integers
Signed integers are used to represent negative values, zero and positive values. As seen earlier, excluding _Bool, there is one signed integer for each type. Variables declared as _Bool can only store the values 0 and 1. Also, the distance between negative and positive numbers will depend on the type of representation.
Historically, in C, it is common to have 3 types of representations for signed int types: a) magnitude and sign; b) complement of one, and; c) complement of two. Let’s look at each of these representations.
- In the sign and magnitude representation, the most significant bit indicates the sign, so the rest of the bits represent the magnitude of the value in binary notation.
- In the complement of one, the value is obtained by reversing all bits in the binary representation of the integer in question. In other words, transforming bit 0 to 1, and bit 1 to 0.
- In the complement of two (the representation that also occurs in binary form) the most significant bit represents the sign. The most significant bit valued zero or 1 represents the positive and negative signs, respectively. The remaining bits are used to represent the magnitude. As in the one’s complement, in the two’s complement, an inversion of all bits is performed and finally another 1 is added to the least significant bit.
Remember that the representation cannot be chosen, since it’s determined by the type of implementation used. Currently, the most used representation is the complement of two. Therefore, we’ll assume this type of representation further on.
Signed integers of size N can have their representation expressed in the range – to -1. So, using an 8-bit signed char as an example, we have a range of -128 to 127. [1]
We still need to define two important terms, Overflow and Underflow. While Overflow represents a value that exceeds the maximum value of a given type, Underflow represents a value smaller than the minimum value allowed.
For the standard, an Overflow in signed integer operations represents undefined behavior. So, it is important to make sure that signed operations never cause an Overflow or Underflow.
Below is a table of operators that can cause an overflow on signed operations:
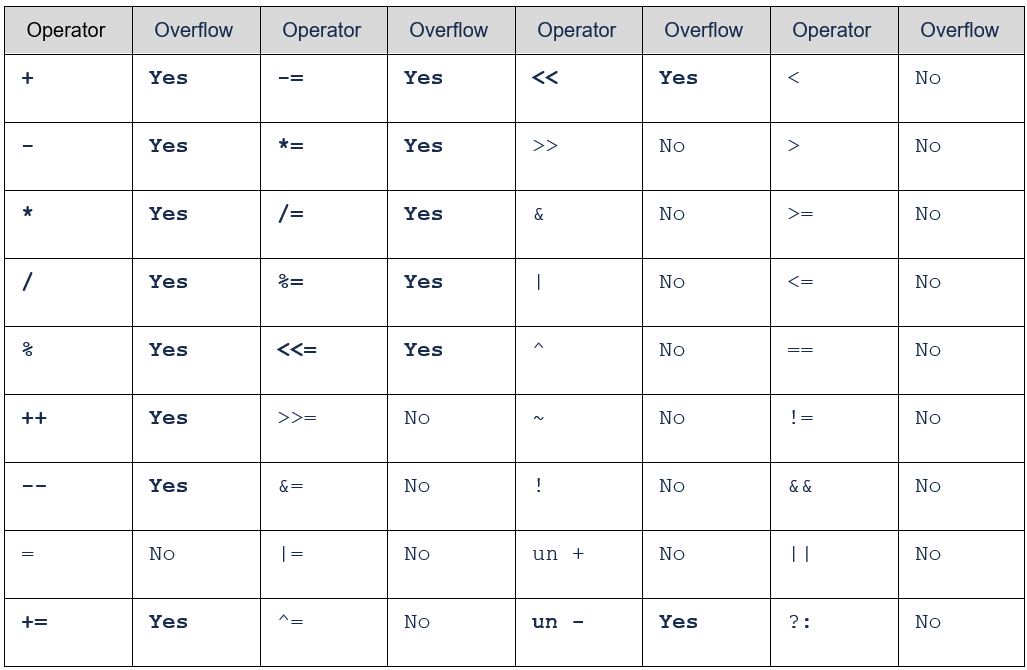
Below are two simple cases of Overflow and Underflow in integers:
Example #04 – Addition
int x = 0x7FFFFFFF;
printf("%d\n", x);
x = x + 1;
printf("%d\n",x);
Code snippet 6: Sum of Unsigned.
Notice that the sum above results in an overflow that exceeds the maximum allowed limit, so the result will be 0x80000000 which is a negative number. As such, here is the result:
2147483647 -2147483648
Example #05 – Subtraction
int x = 0x80000020;
printf("%d\n", x);
x = x - 200;
printf("%d\n", x);
Code snippet 7: Subtraction of Unsigned.
In the case above, on the other hand, the subtraction causes the underflow, since the value will be lower than 0x8000000000000 resulting in a positive number. Below is the result:
-2147483616 2147483480
This way, we see that unsigned integers have a well-defined behavior in wraparound cases. On the other hand, we see that signed integers that generate overflows, or make them possible, should always be considered a defect.
Arithmetic Conversion
Conversions can occur, explicitly, as the result of a cast; or, implicitly, through an operation. In the case of an explicit conversion, it occurs on the demand of whoever wrote that piece of code. Let’s look at the example below:
int x = 10; long z = (long)x;
Code snippet 8: Cast.
A cast is nothing more than the name of the type in parentheses before any expression. The cast converts the original type to the desired type. In the example above, we converted int x to long using cast (long). In this case, we don’t encounter any problems, because an int fits within the representation range of the long type. However, problems start happening when smaller types extrapolate the size into larger types, or even worse, when all this happens without the programmer’s control or permission.
As for implicit conversion, this happens when operations of different types occur. Moreover, we point out that the rules that determine the values to be implicitly converted tend to be complicated. Also, they usually involve the concepts of conversion rank (classification) and promotions of integers, which we’ll study next.
Conversion rank
Each integer type has a conversion rank that will determine when and how conversions will be performed. According to the standard, there are eight rules:
1 – the rank of a signed integer is greater than the rank of any signed integer with less precision; Precision is the number of bits used to represent values, excluding sign and padding.
2- the rank of a long long int is greater than any long int, which is greater than any int, which in turn is greater than any short int, which is greater than any signed char;
3 – the rank of any unsigned char is equivalent to the rank of its signed counterpart;
4 – the rank of a char is equivalent to the rank of a signed char and an unsigned char;
5 – the rank of _Bool is less than the rank of any other integer type;
6 – the rank of any enum type is equivalent to the rank of a compatible type. Every enum type is compatible with char, a signed integer or an unsigned integer;
7 – two signed integers will not have the same rank, even if they have the same representation;
8 – the rank of any extended integer, relative to another extended integer, and with the same precision, will be defined by the implementation.
Integer promotions
Promotion is the process of converting small types into an int or unsigned int. Small type being an integer that has a lower conversion rank than an int or unsigned int.
There are two reasons why the existence of promotions is justified. The first reason is due to processor optimizations, since working with only integer types is always faster. Consequently, the other reason is that it’s possible to avoid overflows in small type operations with larger types.
For each type in C/C++ there is a required alignment, which is mandated by processor architectures. So as not to get into other topics, we should just keep in mind that for most processors it’s more economical to read all 4 bytes of an integer in one memory cycle than, for example, to read 1 byte every cycle. Therefore, the preference is to transform small types into integers.
If a signed integer can represent all the values of the original type, the value is converted to integer; otherwise, the value is converted to unsigned.
Example #6
char a = 30, b = 40, c = 10;
char d = (a * b) / c;
printf ("%d ", d);
return 0;
Code snippet 9: Ar conversion.
Performing the operations manually, we see that d = 30 * 40 = 1200, so that the value of a char (which is from -128 to 127) is exceeded.
Compiling the above code and executing it, we see its output:
output: 120
How can the result be 120? The answer is that the compiler performed a promotion from small type char to integer at the moment of multiplication. So, 1200 is a value that fits inside an integer. For this reason, the division occurs normally, without compiler errors or program crashes. What happened was the division of an integer by a char, so we have no problems at runtime.
Example #7
signed char result, a, b, c; a = 100; b = 3; c = 4; result = a * b / c;
Code snippet 10: Promotion.
As a result, we have that a * b = 300, exceeding the maximum value of a signed char, which is 127. However, due to the promotion, the final result will be 75, and 75 is in the range of a signed char.
To understand arithmetic conversions, you need to understand the operators and the conditions of the conversions. The first operation of an arithmetic conversion is to check if the float type is used within the operation. After that, the following rules apply:
- if a type on one side of the operands is long double, the other operand will be converted to long double;
- otherwise, if a type on one side of the operands is double, the other operand will be converted to double;
- if a type on one side of the operand is float, the other operand will be converted to float;
- otherwise, integer promotions will be performed on both operands..
For example, if one operand is of type double and the other operand is of type int, the int operand is converted to one of type double.
The following rules apply when not dealing with float types:
- when both operands have the same type, no conversion is required;
- otherwise, when both operands have the same sign, the type with the lower rank in the conversion is converted to the type with the higher rank;
- when the operand is of type unsigned and has the rank greater than or equal to the other operand, then the operand with the signed type is converted to the unsigned type;
- when the operand of type signed represents all the values of an operand of type unsigned, the operand of type unsigned will be converted to signed. For example, if one operand is of type unsigned int and the other operand is of type signed long long, if the signed long long can represent all the values of the unsigned int, then the unsigned int will be converted to an object of type signed long long;
- otherwise, both operands are converted to unsigned respecting the type of the signed operand.
Next, we will see some examples of implicit conversion.
Example #8
char a = 0xfb;
unsigned char b = 0xfb;
printf("a = %c", a);
printf("\nb = %c", b);
if (a == b)
printf("\nValores iguais");
else
printf("\nValores diferentes");
Code snippet 11.
When we print on the screen a and b, the same character is printed, but when we compare them, we get different results, even though both are represented as char.
output: Different values
Why does the output of this comparison result in different values?
According to the rules we saw, signed char and unsigned char have the same conversion rank. However, they are small types; therefore, they will be converted to int. Since a signed int holds the promoted values, both the value of a and the value of b will be converted to signed int at the time of comparison. Therefore, a will be equal to -5 and b will be equal to 251, following the wraparound rules. So they are not equal, even though they have the same assigned values.
Example #9
unsigned char a = 255;
unsigned char b = 255;
unsigned char c = a + b;
if (c > 300)
printf("Success!\n");
else
printf("Fail!\n");
Code snippet 12.
In this case, c will be equal to 255 + 255 = 510. The result would already overflow the maximum value of UCHAR_MAX. However, due to the promotion of char to integer, no error occurred. However, at the time of comparison, the value of c will be reduced to the modulus of the maximum value of type plus 1 (510 % 255 + 1 = 254). So, under this condition, the result will be 255 + 255 = 254.
output: Fail!
Example #10
int len = -5;
if (len < sizeof(int))
printf("x\n");
Code snippet 13.
To better understand this example, you must know that the type returned by the sizeof operator is the size_t type, which is an unsigned int type. Variables of the size_t type usually provide sufficient precision with respect to the size of an object. The limit of size_t is set by the macro SIZE_MAX. Thus, we have a comparison of a signed integer with an unsigned integer.
Let’s remember conversion rule number 3, which says: “When the operand is of type unsigned and has the rank greater than or equal to the other operand, then the operand with the signed type is converted to the unsigned type.” So the variable len will be converted to unsigned, assuming a value of 4294967291.
The comparison that actually happens is this:
if ( 4294967291 < sizeof(int))
Code snippet 14.
Example #11
char *buf;
int len = -1;
if (len > 8000) { return 0; }
buf = malloc(len);
read(0, buf, len);
return 0;
Code snippet 15.
Many libraries and their respective functions use some parameter to measure the size of an object, usually using an argument that is of type size_t, for example, like the read function that has the following structure:
size_t read (int fd, void* buf, size_t cnt);
Code snippet 16.
Since the third parameter is the one that determines the size to be read, we see that, in the example above, the len parameter will become of type unsigned. Therefore, it is possible to cause an overflow when reading, because it would be possible to read more bytes than programmed.
So, it’s important to be very careful when using a size as a function parameter, because it will usually be implicitly converted to an unsigned int.
Below is a list of some functions that use the size_t type as size:
ssize_t read(int fd, void *buf, size_t count); void *memcpy(void *dest, const void *src, size_t n); void *malloc(size_t size); int snprintf(char *s, size_t size, const char *fmt, ...); char *strncpy(char *dest, const char *src, size_t n); char *strncat(char *dest, const char *src, size_t n);
Code snippet 17.
Example #12
int read_user_data(int sockfd) {
int length, sockfd, n;
char buffer[1024];
length = get_user_length(sockfd);
if (length > 1024)
return -1;
if (read(sockfd, buffer, length) < 0)
return -1
return 0;
}
Code snippet 18.
Repeating what we saw in example 11, you can see the condition to be bypassed:
if (length > 1024) return -1;
Code snippet 19.
Necessarily, length must be within the limit [INT_MIN; 1024], and then, in the code snippet, the read function is employed, using with size the parameter length. So the read function expects a size from size_t, which in turn is of type unsigned.
So it’s possible to cause a stack overflow, if the number -1 is entered as length: on first check -1 < 1024; then, as length will be transformed to an unsigned int, it will take the value 4294967295.
Example #13
In the example below, we’ll see that it’s possible to cause an overflow by multiplying two unsigned.
unsigned short a = 45000 , b = 50000; unsigned int c = a * b;
Code snippet 20.
The problem occurs when the multiplication takes place, because 45000 * 50000 = 2250000000. Naturally, this value exceeds the maximum value of a short. Therefore, by the conversion rules, the unsigned short will be converted to a signed int, which in turn will also have its maximum value exceeded by the multiplication. So an overflow will occur in a product of two unsigned ones.
Example #14
The description of bug CVE-2015-6575 is as follows:
SampleTable.cpp in libstagefright in Android before 5.1.1 LMY48I does not properly consider integer promotion, which allows remote attackers to execute arbitrary code or cause a denial of service (integer overflow and memory corruption) via crafted atoms in MP4 data
Searching for the vulnerable code snippet, you can observe the following:
mTimeToSampleCount = U32_AT(&header[4]); uint64_t allocSize = mTimeToSampleCount * 2 * sizeof(uint32_t);
Code snippet 21.
We have the mTimeToSampleCount object which gets its value assigned through an unsigned_int32 type. Afterwards, the allocsize object which is of type unsigned long long (whose value is equivalent to that of an unsigned_int64) will have its value assigned through the multiplication of two unsigned objects, since mTimeToSampleCount is unsigned. Because sizeof, as we saw earlier, is of type size_t, which in turn is of type unsigned.
Considering what we saw earlier, the promotion will occur, and if the user enters a very large value, it will overflow.
The suggested fix for this type of unsigned integer multiplication scenario is to force an explicit conversion.
And finally, you can see the fix applied in the Android library:
uint64_t allocSize = mTimeToSampleCount * 2 * (uint64_t)sizeof(uint32_t);
Code snippet 22.
So, we conclude our examples, as well as this study, by verifying that, in this case, using the uint64_t cast, the multiplication will be performed on a larger range that will hold the entered values. Of course, this is only part of the correction, since it is important to validate post multiplication conditions, in order to avoid using unexpected values.
Conclusion
With all this, we emphasize the importance of careful and in-depth study of integers. We believe that the key to preventing vulnerabilities, such as those we have seen, lies in understanding the nuances of the behavior of integers, as well as in their application and implementation in systems.
References
SEACORD, Robert C. Secure Coding in C and C++, 2ª Edição 2013. Addison-Wesley Professional.
SEACORD, Robert C. Effective C An Introduction to Professional C Programming. 2020. NoStarch.
DOWD, Mark; MCDONALD, John; SCHUH, Justin. The Art of Software Security Assessment: Identifying and Preventing Software Vulnerabilities. 2006. Addison-Wesley Professional.
ISO/IEC 9899:2011. INT30-C. Ensure that unsigned integer operations do not wrap. Available at <https://wiki.sei.cmu.edu/confluence/display/c/INT30-C.+Ensure+that+unsigned+integer+operations+do+not+wrap>.
